|
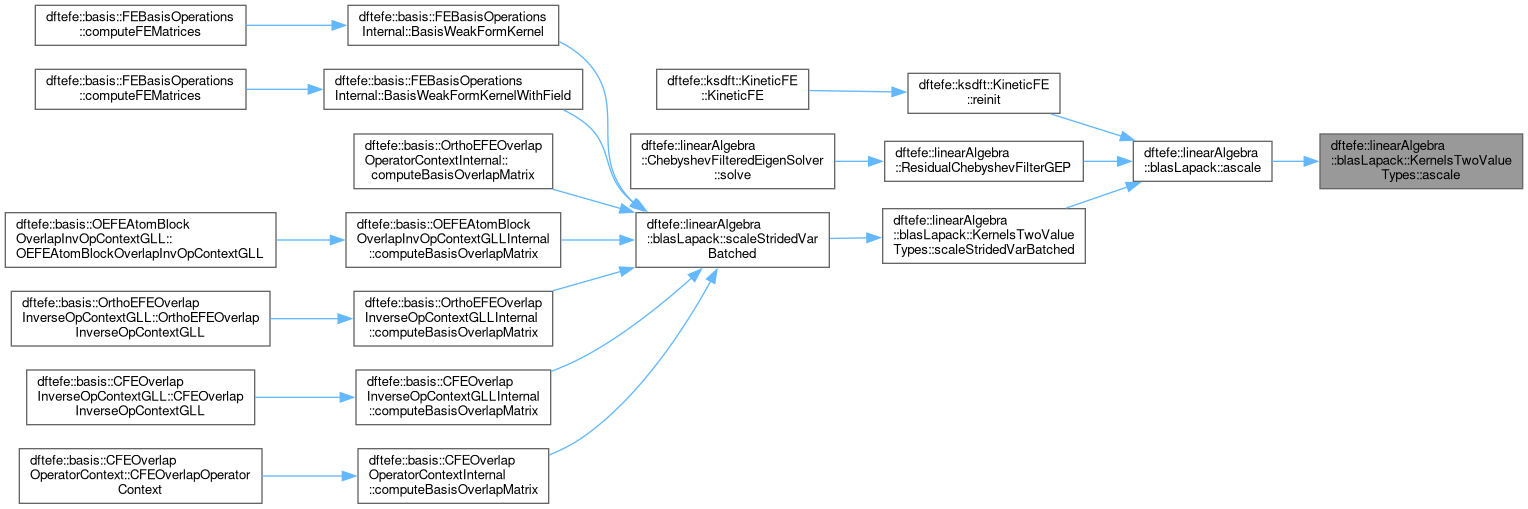
| static void | ascale (size_type size, ValueType1 alpha, const ValueType2 *x, const ScalarOp &opalpha, const ScalarOp &opx, scalar_type< ValueType1, ValueType2 > *z) |
| | Template for performing \( z = \alpha x$
@param[in] size size of the array
@param[in] \) alpha \( scalar
@param[in] x array
@param[out] z array
*/
static void
ascale(size_type size,
ValueType1 alpha,
const ValueType2 * x,
scalar_type<ValueType1, ValueType2> *z);
/**
@brief Template for performing \) z = \alpha x$. More...
|
| |
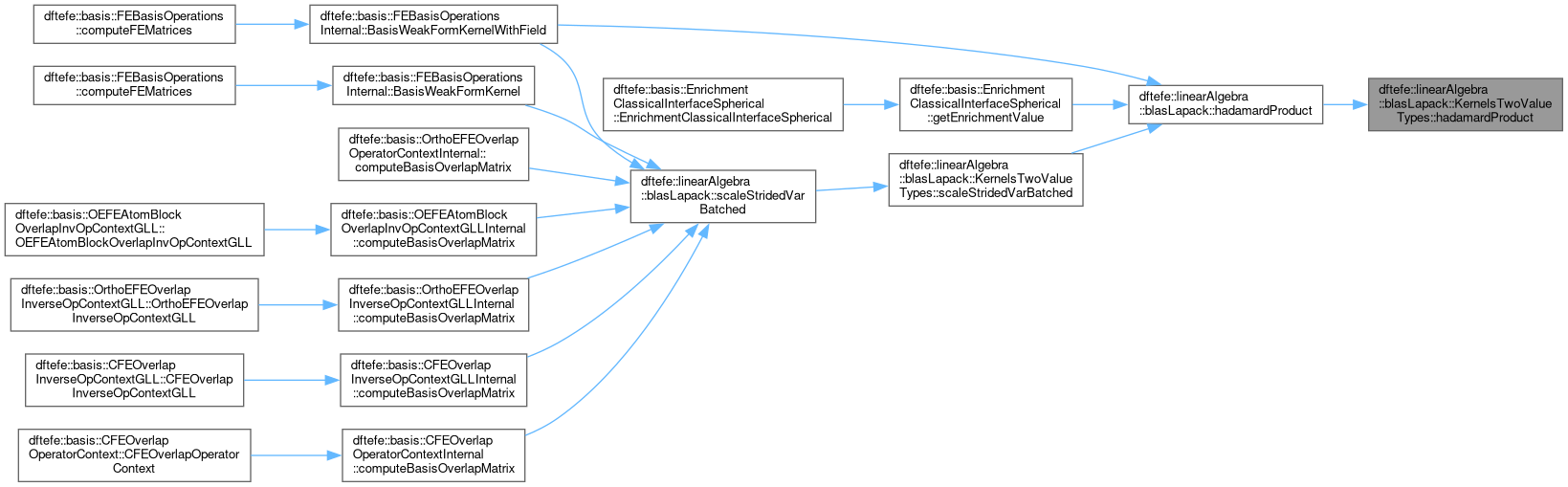
| static void | hadamardProduct (size_type size, const ValueType1 *x, const ValueType2 *y, scalar_type< ValueType1, ValueType2 > *z) |
| | Template for performing \( z = 1 /x$, does not check if x[i] is zero
@param[in] size size of the array
@param[in] x array
@param[out] z array
*/
static void
reciprocalX(size_type size,
const ValueType1 alpha,
const ValueType2 * x,
scalar_type<ValueType1, ValueType2> *z);
/*
@brief Template for performing \) z_i = x_i * y_i$. More...
|
| |
| static void | hadamardProduct (size_type size, const ValueType1 *x, const ValueType2 *y, const ScalarOp &opx, const ScalarOp &opy, scalar_type< ValueType1, ValueType2 > *z) |
| |
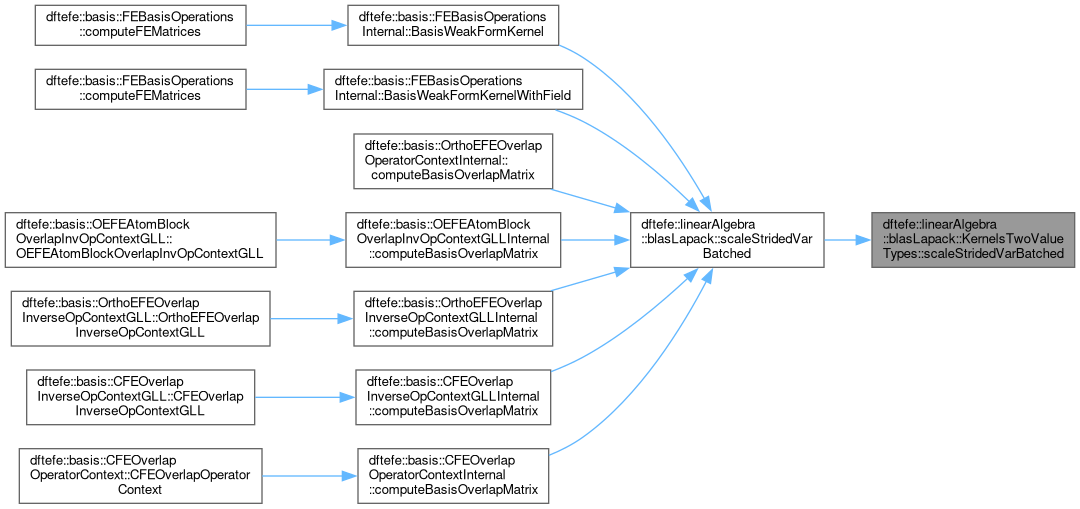
| static void | scaleStridedVarBatched (const size_type numMats, const Layout layout, const ScalarOp &scalarOpA, const ScalarOp &scalarOpB, const size_type *stridea, const size_type *strideb, const size_type *stridec, const size_type *m, const size_type *n, const size_type *k, const ValueType1 *dA, const ValueType2 *dB, scalar_type< ValueType1, ValueType2 > *dC, LinAlgOpContext< memorySpace > &context) |
| | Template for performing hadamard product of two columns of batches of matrix A and B having num col A = m, num common rows = k, num col B = n going through all the rows of A and B with column B having the faster index than columnA. This operation can be thought as the strided form of face-splitting product between two matrices of variable strides but with common rows in each stride. Also it is assumed that the matrices A and B are column major. So for scalarop it represents either identity or complex conjugate operation on a scalar. Size of C on output will be (m*k) cols and n rows with strides. More...
|
| |
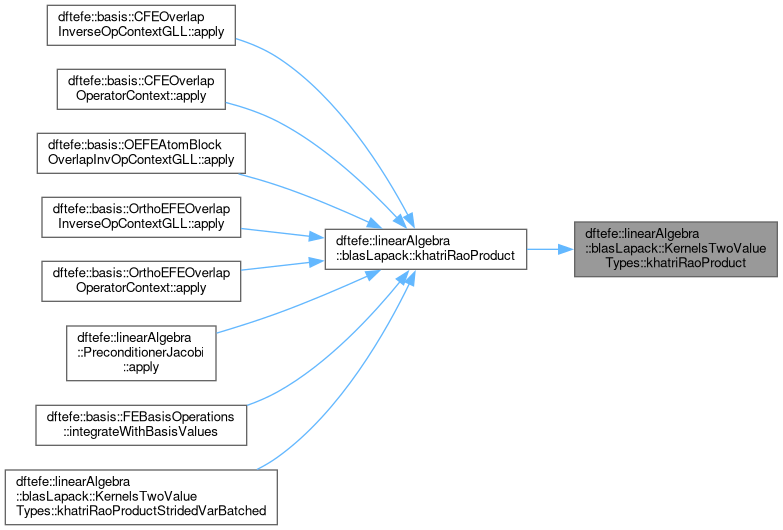
| static void | khatriRaoProduct (const Layout layout, const size_type sizeI, const size_type sizeJ, const size_type sizeK, const ValueType1 *A, const ValueType2 *B, scalar_type< ValueType1, ValueType2 > *Z) |
| | Template for performing In column major storage format: \( {\bf Z}={\bf A} \odot {\bf B} = a_1 \otimes b_1
\quad a_2 \otimes b_2 \cdots \a_K \otimes b_K \), where \({\bf
A}\) is \(I \times K\) matrix, \({\bf B}\) is \(J \times K\), and \(
{\bf Z} \) is \( (IJ)\times K \) matrix. \( a_1 \cdots \a_K \) are the columns of \({\bf A}\) In row major storage format: \( {\bf Z}^T={\bf A}^T \odot {\bf B}^T = a_1 \otimes b_1
\quad a_2 \otimes b_2 \cdots \a_K \otimes b_K \), where \({\bf
A}\) is \(K \times I\) matrix, \({\bf B}\) is \(K \times J\), and \(
{\bf Z} \) is \( K\times (IJ) \) matrix. \( a_1 \cdots \a_K \) are the rows of \({\bf A}\). More...
|
| |
| static void | khatriRaoProductStridedVarBatched (const Layout layout, const size_type numMats, const size_type *stridea, const size_type *strideb, const size_type *stridec, const size_type *m, const size_type *n, const size_type *k, const ValueType1 *dA, const ValueType2 *dB, scalar_type< ValueType1, ValueType2 > *dC, LinAlgOpContext< memorySpace > &context) |
| | Template for performing khatriRao but with variable stride In column major storage format: \( {\bf Z}={\bf A} \odot {\bf B} = a_1 \otimes b_1
\quad a_2 \otimes b_2 \cdots \a_K \otimes b_K \), where \({\bf
A}\) is \(I \times K\) matrix, \({\bf B}\) is \(J \times K\), and \(
{\bf Z} \) is \( (IJ)\times K \) matrix. \( a_1 \cdots \a_K \) are the columns of \({\bf A}\) In row major storage format: \( {\bf Z}^T={\bf A}^T \odot {\bf B}^T = a_1 \otimes b_1
\quad a_2 \otimes b_2 \cdots \a_K \otimes b_K \), where \({\bf
A}\) is \(K \times I\) matrix, \({\bf B}\) is \(K \times J\), and \(
{\bf Z} \) is \( K\times (IJ) \) matrix. \( a_1 \cdots \a_K \) are the rows of \({\bf A}\). More...
|
| |
| static void | transposedKhatriRaoProduct (const Layout layout, const size_type sizeI, const size_type sizeJ, const size_type sizeK, const ValueType1 *A, const ValueType2 *B, scalar_type< ValueType1, ValueType2 > *Z) |
| | Template for performing In column major storage format: \( {\bf Z}={\bf A} \odot {\bf B} = a_1 \otimes b_1
\quad a_2 \otimes b_2 \cdots \a_K \otimes b_K \), where \({\bf
A}\) is \(K \times I\) matrix, \({\bf B}\) is \(K \times J\), and \(
{\bf Z} \) is \( K\times (IJ) \) matrix. \( a_1 \cdots \a_K \) are the rows of \({\bf A}\) In row major storage format: \( {\bf Z}^T={\bf A}^T \odot {\bf B}^T = a_1 \otimes b_1
\quad a_2 \otimes b_2 \cdots \a_K \otimes b_K \), where \({\bf
A}\) is \(I \times K\) matrix, \({\bf B}\) is \(J \times K\), and \(
{\bf Z} \) is \( (IJ)\times K \) matrix. \( a_1 \cdots \a_K \) are the columns of \({\bf A}\). More...
|
| |
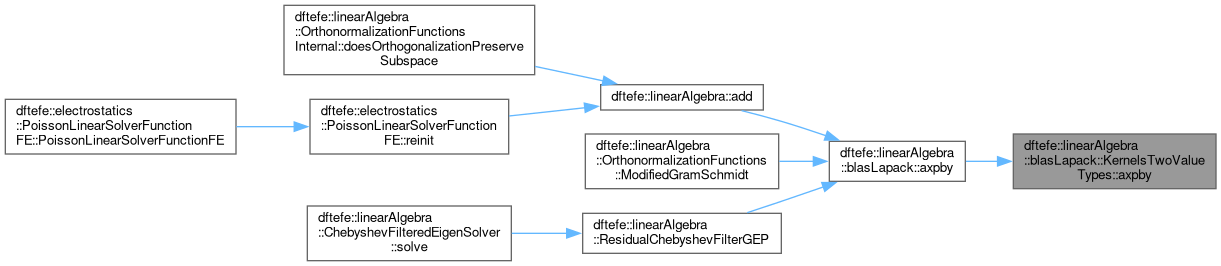
| static void | axpby (size_type size, scalar_type< ValueType1, ValueType2 > alpha, const ValueType1 *x, scalar_type< ValueType1, ValueType2 > beta, const ValueType2 *y, scalar_type< ValueType1, ValueType2 > *z) |
| | Template for performing \( z = \alpha x + \beta y \). More...
|
| |
| static void | axpbyBlocked (const size_type size, const size_type blockSize, const scalar_type< ValueType1, ValueType2 > alpha1, const scalar_type< ValueType1, ValueType2 > *alpha, const ValueType1 *x, const scalar_type< ValueType1, ValueType2 > beta1, const scalar_type< ValueType1, ValueType2 > *beta, const ValueType2 *y, scalar_type< ValueType1, ValueType2 > *z) |
| | Template for performing \( z = \alpha x + \beta y \). More...
|
| |
| static void | dotMultiVector (size_type vecSize, size_type numVec, const ValueType1 *multiVecDataX, const ValueType2 *multiVecDataY, const ScalarOp &opX, const ScalarOp &opY, scalar_type< ValueType1, ValueType2 > *multiVecDotProduct, LinAlgOpContext< memorySpace > &context) |
| | Template for computing dot products numVec vectors in a multi Vector. More...
|
| |
template<typename ValueType1, typename ValueType2,
dftefe::utils::MemorySpace memorySpace>
class dftefe::linearAlgebra::blasLapack::KernelsTwoValueTypes< ValueType1, ValueType2, memorySpace >
namespace class for BlasLapack kernels not present in blaspp.