DFT-EFE
 
Loading...
Searching...
No Matches
Public Member Functions | Private Member Functions | Private Attributes | List of all members
dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType > Class Template Reference

Scalapack wrapper adapted from dealii library and extended implementation to complex datatype. More...

#include <ScalapackWrapper.h>

Public Member Functions

 ScaLAPACKMatrix (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)
 
 ScaLAPACKMatrix (const size_type size, const std::shared_ptr< const ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::hermitian)
 
 ~ScaLAPACKMatrix ()=default
 
void reinit (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)
 
void reinit (const size_type size, const std::shared_ptr< const ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::hermitian)
 
void set_property (const LAPACKSupport::Property property)
 
LAPACKSupport::Property get_property () const
 
LAPACKSupport::State get_state () const
 
void copy_to (ScaLAPACKMatrix< NumberType > &dest) const
 
void conjugate ()
 
void add (const ScaLAPACKMatrix< NumberType > &B, const NumberType a=0., const NumberType b=1., const bool transpose_B=false)
 
void zadd (const ScaLAPACKMatrix< NumberType > &B, const NumberType a=0., const NumberType b=1., const bool conjugate_transpose_B=false)
 
void copy_transposed (const ScaLAPACKMatrix< NumberType > &B)
 
void copy_conjugate_transposed (const ScaLAPACKMatrix< NumberType > &B)
 
void mult (const NumberType b, const ScaLAPACKMatrix< NumberType > &B, const NumberType c, ScaLAPACKMatrix< NumberType > &C, const bool transpose_A=false, const bool transpose_B=false) const
 
void zmult (const NumberType b, const ScaLAPACKMatrix< NumberType > &B, const NumberType c, ScaLAPACKMatrix< NumberType > &C, const bool conjugate_transpose_A=false, const bool conjugate_transpose_B=false) const
 
void mmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void Tmmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void mTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void TmTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void zmmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void zCmmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void zmCmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
void zCmCmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
 
size_type m () const
 
size_type n () const
 
unsigned int local_m () const
 
unsigned int local_n () const
 
unsigned int global_row (const unsigned int loc_row) const
 
unsigned int global_column (const unsigned int loc_column) const
 
NumberType local_el (const unsigned int loc_row, const unsigned int loc_column) const
 
NumberType & local_el (const unsigned int loc_row, const unsigned int loc_column)
 
ScalapackError compute_cholesky_factorization ()
 
ScalapackError compute_lu_factorization ()
 
ScalapackError invert ()
 
void scale_columns (const std::vector< NumberType > &factors)
 
void scale_rows (const std::vector< NumberType > &factors)
 
void scale_columns_realfactors (const std::vector< double > &factors)
 
void scale_rows_realfactors (const std::vector< double > &factors)
 
std::vector< double > eigenpairs_hermitian_by_index (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors, ScalapackError &scalapackError)
 
std::vector< double > eigenpairs_hermitian_by_index_MRRR (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors, ScalapackError &scalapackError)
 

Private Member Functions

std::vector< double > eigenpairs_hermitian (const bool compute_eigenvectors, ScalapackError &scalapackError, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(std::numeric_limits< unsigned int >::max(), std::numeric_limits< unsigned int >::max()), const std::pair< double, double > &value_limits=std::make_pair(std::numeric_limits< double >::quiet_NaN(), std::numeric_limits< double >::quiet_NaN()))
 
std::vector< double > eigenpairs_hermitian_MRRR (const bool compute_eigenvectors, ScalapackError &scalapackError, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(std::numeric_limits< unsigned int >::max(), std::numeric_limits< unsigned int >::max()), const std::pair< double, double > &value_limits=std::make_pair(std::numeric_limits< double >::quiet_NaN(), std::numeric_limits< double >::quiet_NaN()))
 

Private Attributes

std::vector< NumberType > values
 
LAPACKSupport::State state
 
LAPACKSupport::Property property
 
std::shared_ptr< const ProcessGrid > grid
 
int n_rows
 
int n_columns
 
int row_block_size
 
int column_block_size
 
int n_local_rows
 
int n_local_columns
 
int descriptor [9]
 
std::vector< NumberType > work
 
std::vector< int > iwork
 
std::vector< int > ipiv
 
const char uplo
 
const int first_process_row
 
const int first_process_column
 
const int submatrix_row
 
const int submatrix_column
 

Detailed Description

template<typename NumberType>
class dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >

Scalapack wrapper adapted from dealii library and extended implementation to complex datatype.

Author
Sambit Das , Avirup Sircar

Constructor & Destructor Documentation

◆ ScaLAPACKMatrix() [1/2]

template<typename NumberType >
dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix ( const size_type  n_rows,
const size_type  n_columns,
const std::shared_ptr< const ProcessGrid > &  process_grid,
const size_type  row_block_size = 32,
const size_type  column_block_size = 32,
const LAPACKSupport::Property  property = LAPACKSupport::Property::general 
)

Constructor for a rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of $2$, e.g. $16,32,64, \dots$.

Here is the call graph for this function:

◆ ScaLAPACKMatrix() [2/2]

template<typename NumberType >
dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix ( const size_type  size,
const std::shared_ptr< const ProcessGrid > &  process_grid,
const size_type  block_size = 32,
const LAPACKSupport::Property  property = LAPACKSupport::Property::hermitian 
)

Constructor for a square matrix of size size, and distributed using the process grid in process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of $2$, e.g. $16,32,64, \dots$.

◆ ~ScaLAPACKMatrix()

template<typename NumberType >
dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::~ScaLAPACKMatrix ( )
default

Destructor.

Member Function Documentation

◆ add()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::add ( const ScaLAPACKMatrix< NumberType > &  B,
const NumberType  a = 0.,
const NumberType  b = 1.,
const bool  transpose_B = false 
)

The operations based on the input parameter transpose_B and the alignment conditions are summarized in the following table:

transpose_B Block Sizes Operation
false $MB_A=MB_B$
$NB_A=NB_B$ 		$\mathbf{A} = a \mathbf{A} + b \mathbf{B}$
true $MB_A=NB_B$
$NB_A=MB_B$ 		$\mathbf{A} = a \mathbf{A} + b \mathbf{B}^T$

The matrices $\mathbf{A}$ and $\mathbf{B}$ must have the same process grid.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ compute_cholesky_factorization()

template<typename NumberType >
ScalapackError dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::compute_cholesky_factorization

Compute the Cholesky factorization of the matrix using ScaLAPACK function pXpotrf. The result of the factorization is stored in this object.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ compute_lu_factorization()

template<typename NumberType >
ScalapackError dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::compute_lu_factorization

Compute the LU factorization of the matrix using ScaLAPACK function pXgetrf and partial pivoting with row interchanges. The result of the factorization is stored in this object.

Here is the call graph for this function:

◆ conjugate()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::conjugate

Complex conjugate.

Here is the call graph for this function:

◆ copy_conjugate_transposed()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::copy_conjugate_transposed ( const ScaLAPACKMatrix< NumberType > &  B)

Transposing assignment: $\mathbf{A} = \mathbf{B}^C$

The matrices $\mathbf{A}$ and $\mathbf{B}$ must have the same process grid.

The following alignment conditions have to be fulfilled: $MB_A=NB_B$ and $NB_A=MB_B$.

Here is the caller graph for this function:

◆ copy_to()

template<typename NumberType >
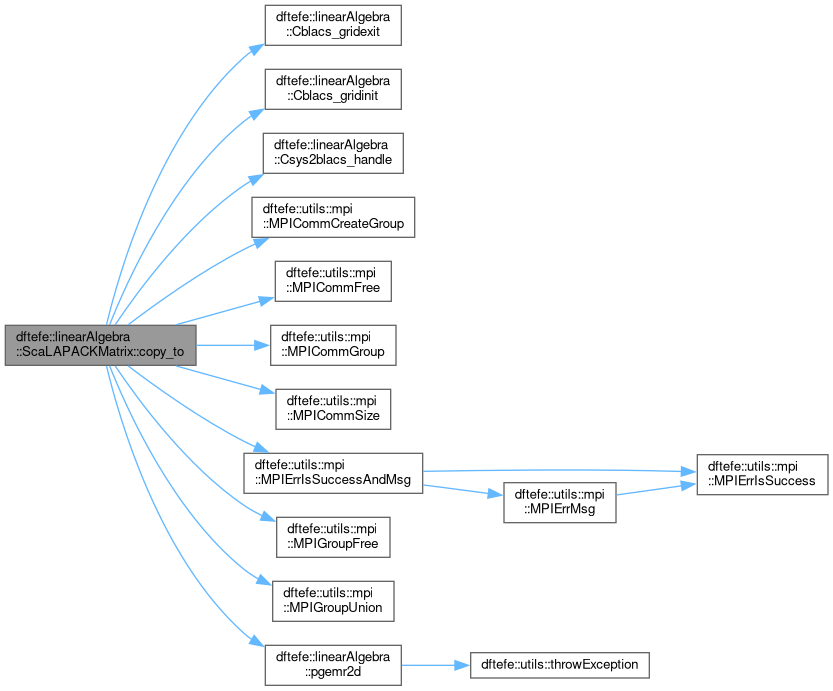
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::copy_to ( ScaLAPACKMatrix< NumberType > &  dest) const

Copy the contents of the distributed matrix into a differently distributed matrix dest. The function also works for matrices with different process grids or block-cyclic distributions.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ copy_transposed()

template<typename NumberType >
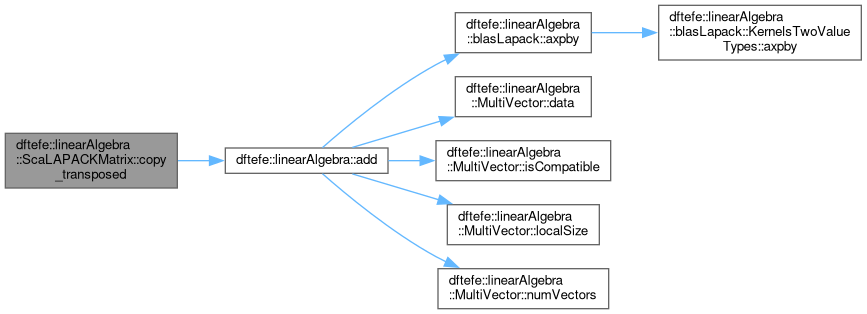
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::copy_transposed ( const ScaLAPACKMatrix< NumberType > &  B)

Transposing assignment: $\mathbf{A} = \mathbf{B}^T$

The matrices $\mathbf{A}$ and $\mathbf{B}$ must have the same process grid.

The following alignment conditions have to be fulfilled: $MB_A=NB_B$ and $NB_A=MB_B$.

Here is the call graph for this function:

◆ eigenpairs_hermitian()

template<typename NumberType >
std::vector< double > dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::eigenpairs_hermitian ( const bool  compute_eigenvectors,
ScalapackError &  scalapackError,
const std::pair< unsigned int, unsigned int > &  index_limits = std::make_pair(std::numeric_limits<unsigned int>::max(),                         std::numeric_limits<unsigned int>::max()),
const std::pair< double, double > &  value_limits = std::make_pair(std::numeric_limits<double>::quiet_NaN(),                         std::numeric_limits<double>::quiet_NaN()) 
)
private

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited. If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Here is the call graph for this function:

◆ eigenpairs_hermitian_by_index()

template<typename NumberType >
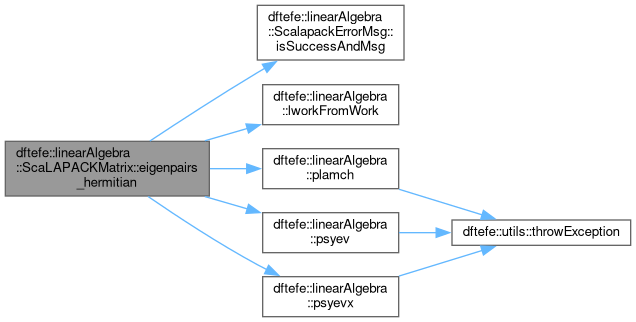
std::vector< double > dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::eigenpairs_hermitian_by_index ( const std::pair< unsigned int, unsigned int > &  index_limits,
const bool  compute_eigenvectors,
ScalapackError &  scalapackError 
)

Computing selected eigenvalues and, optionally, the eigenvectors of the real hermitian matrix $\mathbf{A} \in \mathbb{R}^{M \times M}$.

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval $ \left[ 0, M-1 \right] $ in index_limits.

Pass the closed interval $ \left[ M-r, M-1 \right] $ if the $r$ largest eigenvalues/eigenvectors are desired.

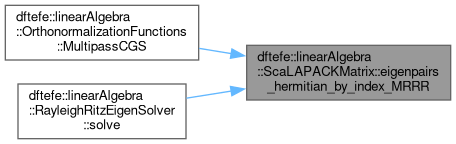
◆ eigenpairs_hermitian_by_index_MRRR()

template<typename NumberType >
std::vector< double > dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::eigenpairs_hermitian_by_index_MRRR ( const std::pair< unsigned int, unsigned int > &  index_limits,
const bool  compute_eigenvectors,
ScalapackError &  scalapackError 
)

Computing selected eigenvalues and, optionally, the eigenvectors of the real hermitian matrix $\mathbf{A} \in \mathbb{R}^{M \times M}$ using the MRRR algorithm.

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval $ \left[ 0, M-1 \right] $ in index_limits.

Pass the closed interval $ \left[ M-r, M-1 \right] $ if the $r$ largest eigenvalues/eigenvectors are desired.

Here is the caller graph for this function:

◆ eigenpairs_hermitian_MRRR()

template<typename NumberType >
std::vector< double > dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::eigenpairs_hermitian_MRRR ( const bool  compute_eigenvectors,
ScalapackError &  scalapackError,
const std::pair< unsigned int, unsigned int > &  index_limits = std::make_pair(std::numeric_limits<unsigned int>::max(),                         std::numeric_limits<unsigned int>::max()),
const std::pair< double, double > &  value_limits = std::make_pair(std::numeric_limits<double>::quiet_NaN(),                         std::numeric_limits<double>::quiet_NaN()) 
)
private

Computing selected eigenvalues and, optionally, the eigenvectors of the real hermitian matrix $\mathbf{A} \in \mathbb{R}^{M \times M}$ using the MRRR algorithm. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited.

By calling this function the original content of the matrix will be overwritten. If requested, the eigenvectors are stored in the columns of the matrix. Also in the case that just the eigenvalues are required, the content of the matrix will be overwritten.

If successful, the computed eigenvalues are arranged in ascending order.

Note
Due to a bug in Netlib-ScaLAPACK, either all or no eigenvectors can be computed. Therefore, the input index_limits has to be set accordingly. Using Intel-MKL this restriction is not required.
Here is the call graph for this function:

◆ get_property()

template<typename NumberType >
LAPACKSupport::Property dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::get_property

Return current property of this matrix

Here is the caller graph for this function:

◆ get_state()

template<typename NumberType >
LAPACKSupport::State dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::get_state

Return current state of this matrix

◆ global_column()

template<typename NumberType >
unsigned int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::global_column ( const unsigned int  loc_column) const

Return the global column number for the given local column loc_column.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ global_row()

template<typename NumberType >
unsigned int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::global_row ( const unsigned int  loc_row) const

Return the global row number for the given local row loc_row .

Here is the call graph for this function:
Here is the caller graph for this function:

◆ invert()

template<typename NumberType >
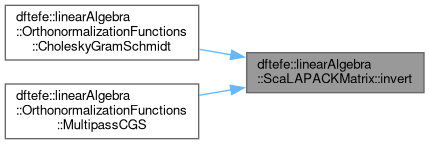
ScalapackError dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::invert

Invert the matrix by first computing a Cholesky for hermitian matrices or a LU factorization for general matrices and then building the actual inverse using pXpotri or pXgetri. If the matrix is triangular, the LU factorization step is skipped, and pXtrtri is used directly.

If a Cholesky or LU factorization has been applied previously, pXpotri or pXgetri are called directly.

The inverse is stored in this object.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ local_el() [1/2]

template<typename NumberType >
NumberType & dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::local_el ( const unsigned int  loc_row,
const unsigned int  loc_column 
)
inline

Write access to local element.

◆ local_el() [2/2]

template<typename NumberType >
NumberType dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::local_el ( const unsigned int  loc_row,
const unsigned int  loc_column 
) const
inline

Read access to local element.

Here is the caller graph for this function:

◆ local_m()

template<typename NumberType >
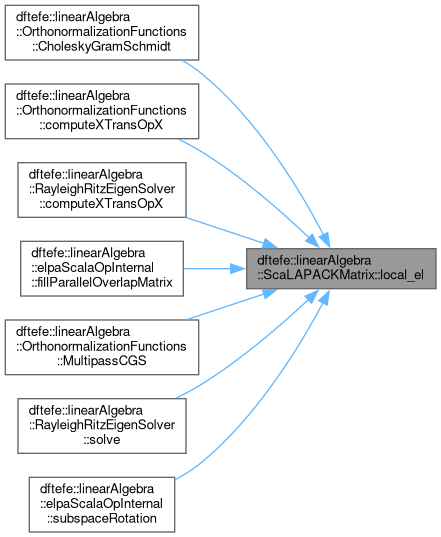
unsigned int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::local_m

Number of local rows on this MPI processes.

Here is the caller graph for this function:

◆ local_n()

template<typename NumberType >
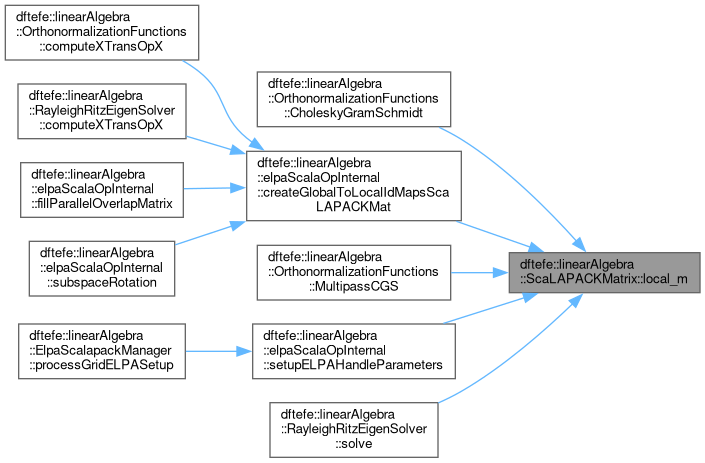
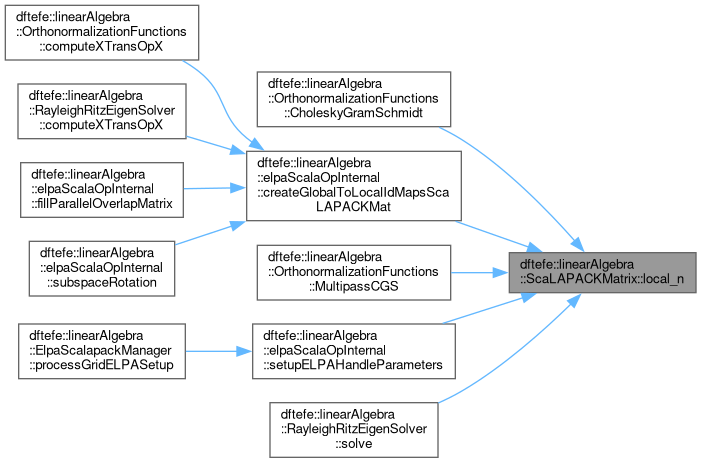
unsigned int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::local_n

Number of local columns on this MPI process.

Here is the caller graph for this function:

◆ m()

template<typename NumberType >
unsigned int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::m
inline

Number of rows of the $M \times N$ matrix.

◆ mmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::mmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}$

else $\mathbf{C} = \mathbf{A} \cdot \mathbf{B}$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=MB_C$, $NB_A=MB_B$ and $NB_B=NB_C$.

◆ mTmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::mTmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication using the transpose of $\mathbf{B}$.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}^T$

else $\mathbf{C} = \mathbf{A} \cdot \mathbf{B}^T$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=MB_C$, $NB_A=NB_B$ and $MB_B=NB_C$.

◆ mult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::mult ( const NumberType  b,
const ScaLAPACKMatrix< NumberType > &  B,
const NumberType  c,
ScaLAPACKMatrix< NumberType > &  C,
const bool  transpose_A = false,
const bool  transpose_B = false 
) const

Matrix-matrix-multiplication:

The operations based on the input parameters and the alignment conditions are summarized in the following table:

transpose_A transpose_B Block Sizes Operation
false false $MB_A=MB_C$
$NB_A=MB_B$
$NB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A} \cdot \mathbf{B} + c \mathbf{C}$
false true $MB_A=MB_C$
$NB_A=NB_B$
$MB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A} \cdot \mathbf{B}^T + c \mathbf{C}$
true false $MB_A=MB_B$
$NB_A=MB_C$
$NB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B} + c \mathbf{C}$
true true $MB_A=NB_B$
$NB_A=MB_C$
$MB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B}^T + c \mathbf{C}$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The matrices $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ must have the same process grid.

Here is the call graph for this function:

◆ n()

template<typename NumberType >
unsigned int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::n
inline

Number of columns of the $M \times N$ matrix.

◆ reinit() [1/2]

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::reinit ( const size_type  n_rows,
const size_type  n_columns,
const std::shared_ptr< const ProcessGrid > &  process_grid,
const size_type  row_block_size = 32,
const size_type  column_block_size = 32,
const LAPACKSupport::Property  property = LAPACKSupport::Property::general 
)

Initialize the rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of $2$, e.g. $16,32,64, \dots$.

Here is the call graph for this function:
Here is the caller graph for this function:

◆ reinit() [2/2]

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::reinit ( const size_type  size,
const std::shared_ptr< const ProcessGrid > &  process_grid,
const size_type  block_size = 32,
const LAPACKSupport::Property  property = LAPACKSupport::Property::hermitian 
)

Initialize the square matrix of size size and distributed using the grid process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of $2$, e.g. $16,32,64, \dots$.

◆ scale_columns()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::scale_columns ( const std::vector< NumberType > &  factors)

Scale the columns of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix columns.

Copies of factors have to be available on all processes of the underlying MPI communicator.

◆ scale_columns_realfactors()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::scale_columns_realfactors ( const std::vector< double > &  factors)

Scale the columns of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix columns.

Copies of factors have to be available on all processes of the underlying MPI communicator.

◆ scale_rows()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::scale_rows ( const std::vector< NumberType > &  factors)

Scale the rows of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix rows.

Copies of factors have to be available on all processes of the underlying MPI communicator.

◆ scale_rows_realfactors()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::scale_rows_realfactors ( const std::vector< double > &  factors)

Scale the rows of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix rows.

Copies of factors have to be available on all processes of the underlying MPI communicator.

◆ set_property()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::set_property ( const LAPACKSupport::Property  property)

Assign property to this matrix.

◆ Tmmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::Tmmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication using transpose of $\mathbf{A}$.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}$

else $\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=MB_B$, $NB_A=MB_C$ and $NB_B=NB_C$.

◆ TmTmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::TmTmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication using transpose of $\mathbf{A}$ and $\mathbf{B}$.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}^T$

else $\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}^T$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=NB_B$, $NB_A=MB_C$ and $MB_B=NB_C$.

◆ zadd()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::zadd ( const ScaLAPACKMatrix< NumberType > &  B,
const NumberType  a = 0.,
const NumberType  b = 1.,
const bool  conjugate_transpose_B = false 
)

The operations based on the input parameter conjugate_transpose_B and the alignment conditions are summarized in the following table:

transpose_B Block Sizes Operation
false $MB_A=MB_B$
$NB_A=NB_B$ 		$\mathbf{A} = a \mathbf{A} + b \mathbf{B}$
true $MB_A=NB_B$
$NB_A=MB_B$ 		$\mathbf{A} = a \mathbf{A} + b \mathbf{B}^C$

The matrices $\mathbf{A}$ and $\mathbf{B}$ must have the same process grid.

Here is the call graph for this function:

◆ zCmCmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::zCmCmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication using conjugate transpose of $\mathbf{A}$ and $\mathbf{B}$.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A}^C \cdot \mathbf{B}^T$

else $\mathbf{C} = \mathbf{A}^C \cdot \mathbf{B}^C$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=NB_B$, $NB_A=MB_C$ and $MB_B=NB_C$.

◆ zCmmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::zCmmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication using conjugate transpose of $\mathbf{A}$.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A}^C \cdot \mathbf{B}$

else $\mathbf{C} = \mathbf{A}^C \cdot \mathbf{B}$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=MB_B$, $NB_A=MB_C$ and $NB_B=NB_C$.

◆ zmCmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::zmCmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication using the conjugate transpose of $\mathbf{B}$.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}^C$

else $\mathbf{C} = \mathbf{A} \cdot \mathbf{B}^C$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=MB_C$, $NB_A=NB_B$ and $MB_B=NB_C$.

◆ zmmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::zmmult ( ScaLAPACKMatrix< NumberType > &  C,
const ScaLAPACKMatrix< NumberType > &  B,
const bool  adding = false 
) const

Matrix-matrix-multiplication.

The optional parameter adding determines whether the result is stored in $\mathbf{C}$ or added to $\mathbf{C}$.

if (adding) $\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}$

else $\mathbf{C} = \mathbf{A} \cdot \mathbf{B}$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The following alignment conditions have to be fulfilled: $MB_A=MB_C$, $NB_A=MB_B$ and $NB_B=NB_C$.

◆ zmult()

template<typename NumberType >
void dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::zmult ( const NumberType  b,
const ScaLAPACKMatrix< NumberType > &  B,
const NumberType  c,
ScaLAPACKMatrix< NumberType > &  C,
const bool  conjugate_transpose_A = false,
const bool  conjugate_transpose_B = false 
) const

Matrix-matrix-multiplication:

The operations based on the input parameters and the alignment conditions are summarized in the following table:

conjugate_transpose_A conjugate_transpose_B Block Sizes Operation
false false $MB_A=MB_C$
$NB_A=MB_B$
$NB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A} \cdot \mathbf{B} + c \mathbf{C}$
false true $MB_A=MB_C$
$NB_A=NB_B$
$MB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A} \cdot \mathbf{B}^C + c \mathbf{C}$
true false $MB_A=MB_B$
$NB_A=MB_C$
$NB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A}^C \cdot \mathbf{B} + c \mathbf{C}$
true true $MB_A=NB_B$
$NB_A=MB_C$
$MB_B=NB_C$ 		$\mathbf{C} = b \mathbf{A}^C \cdot \mathbf{B}^C + c \mathbf{C}$

It is assumed that $\mathbf{A}$ and $\mathbf{B}$ have compatible sizes and that $\mathbf{C}$ already has the right size.

The matrices $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ must have the same process grid.

Here is the call graph for this function:

Member Data Documentation

◆ column_block_size

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::column_block_size
private

Column block size.

◆ descriptor

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::descriptor[9]
private

ScaLAPACK description vector.

◆ first_process_column

template<typename NumberType >
const int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::first_process_column
private

The process column of the process grid over which the first column of the global matrix is distributed.

◆ first_process_row

template<typename NumberType >
const int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::first_process_row
private

The process row of the process grid over which the first row of the global matrix is distributed.

◆ grid

template<typename NumberType >
std::shared_ptr<const ProcessGrid> dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::grid
private

A shared pointer to a MPI::ProcessGrid object which contains a BLACS context and a MPI communicator, as well as other necessary data structures.

◆ ipiv

template<typename NumberType >
std::vector<int> dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::ipiv
private

Integer array holding pivoting information required by ScaLAPACK's matrix factorization routines.

◆ iwork

template<typename NumberType >
std::vector<int> dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::iwork
mutableprivate

Integer workspace array.

◆ n_columns

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::n_columns
private

Number of columns in the matrix.

◆ n_local_columns

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::n_local_columns
private

Number of columns in the matrix owned by the current process.

◆ n_local_rows

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::n_local_rows
private

Number of rows in the matrix owned by the current process.

◆ n_rows

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::n_rows
private

Number of rows in the matrix.

◆ property

template<typename NumberType >
LAPACKSupport::Property dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::property
private

Additional property of the matrix which may help to select more efficient ScaLAPACK functions.

◆ row_block_size

template<typename NumberType >
int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::row_block_size
private

Row block size.

◆ state

template<typename NumberType >
LAPACKSupport::State dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::state
private

Since ScaLAPACK operations notoriously change the meaning of the matrix entries, we record the current state after the last operation here.

◆ submatrix_column

template<typename NumberType >
const int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::submatrix_column
private

Global column index that determines where to start a submatrix. Currently this equals unity, as we don't use submatrices.

◆ submatrix_row

template<typename NumberType >
const int dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::submatrix_row
private

Global row index that determines where to start a submatrix. Currently this equals unity, as we don't use submatrices.

◆ uplo

template<typename NumberType >
const char dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::uplo
private

A character to define where elements are stored in case ScaLAPACK operations support this.

◆ values

template<typename NumberType >
std::vector<NumberType> dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::values
private

local storage

◆ work

template<typename NumberType >
std::vector<NumberType> dftefe::linearAlgebra::ScaLAPACKMatrix< NumberType >::work
mutableprivate

Workspace array.

The documentation for this class was generated from the following files: